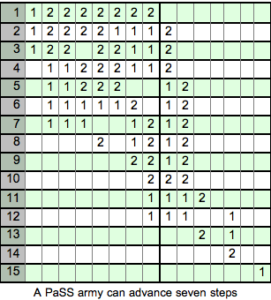
How far can a model army advance into a one-dimensional desert, using only finite resources and prescribed types of movement? Over the past five weeks Gustavus Juniors Filip Belik and Ha Le, have been investigating the logistics and limits of movement in a formal system called Port-and-Sweep Solitaire, which can be regarded as a more complex variant of the classic peg solitaire puzzle.
Belik and Le have shown that an advance of seven spaces in the model is possible, and that advances of nine or more spaces are impossible. Their work adapts ideas from analogous problems considered by John Conway and others in the realm of peg solitaire, making use of a variety of techniques from pure and computational mathematics. The real root of the polynomial 2x^3 – x^2 – x – 1 turns out to play a large role in the analysis.
The question of whether an advance of eight spaces is possible is still under consideration. Partial results give strong evidence that the answer is “no,” but an airtight proof remains elusive.
Belik and Le have been working under the supervision of Mathematics Professor Dr. Jacob Siehler. Their work has been funded by the Steve Hilding fund. You can learn more about Port-and-Sweep Solitaire and other challenging puzzles by visiting Professor Siehler’s web page.